双有理几何基础之linear system 上的positivity 以及 Kodaira vanishing theorem 的推论们. 全文抄写自Lazarsfeld 的Positivity in Algebraic Geometry, 不含任何一点原创. 属于是假期闲着无聊想了解下Minimal Model Program 时的一些前置知识. 最重要的部分还是最后一节关于一些有效消失定理们.
人生苦短 不如摸鱼
天道几何 万品流形先自守 变分无限 孤心测度有同伦
Descent Theory
摘抄自Stack Project 和J. Alper 的stack and moduli. Descent theory 主旨在于如何进行base change的逆过程. 最重要的结果便是faithful flat morphism 可以induce 出category of quasi-coherent sheaves 和category of quasi-coherent sheaves with descent data 的等价, 进而导出一系列morphism 上的性质. 在moduli theory 中descent theory 主要用于gluing data.
Etale Slice Theorem
Presentation 定理, 证明并不完善, 缺少其中最重要的引理的证明. Etale slice theorem 是用于研究GIT quotient 局部性质的很好工具. 它将GIT quotient 和其上的principal bundle 局部作了一个对应, 并且给出了一个local etale trivialization.
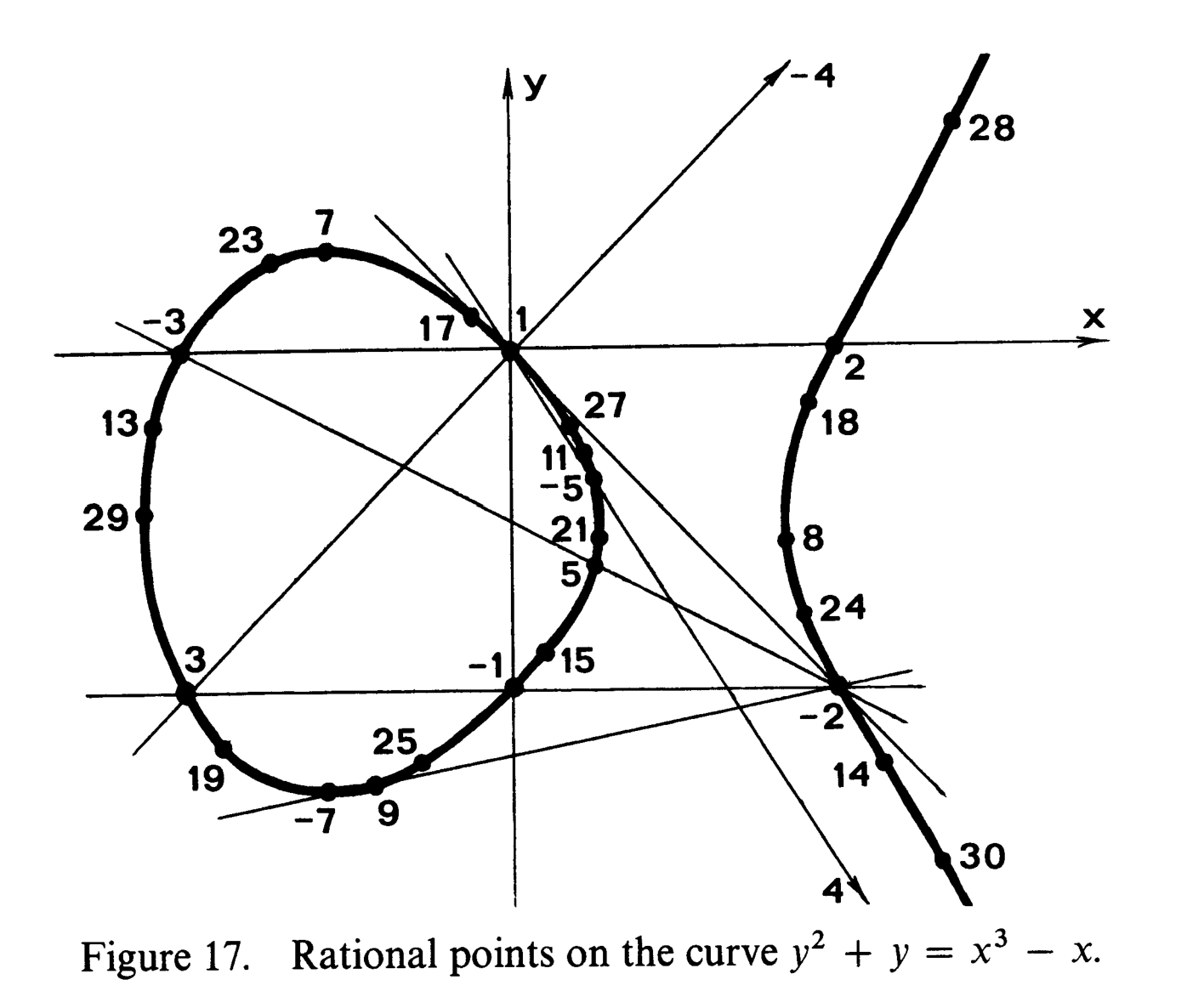
Hasse Weil Bound
宝宝巴士第一集: 学会Riemann Hypothesis.
宝宝巴士第二集: 证明Hasse Weil Bound.
宝宝巴士第三集: 证明nonsingular curve上的Riemann Hypothesis.
宝宝巴士第四集: 证明Weil Conjecture.
Boundedness of Semistable Sheaves
本文为2024年暑假我于HKUST作的summer research program报告chaoshubiji. 在此我希望对港科的Li Weiping老师表示由衷的感谢. Li教授在代数几何方面学问广博, 平易近人, 他的教学深明大义, 向我揭示了模空间这一宏伟理论的一隅. 我因为水平有限, 难以形成自己的成果, 只能抄书作为报告, 实在惭愧.
以下是introduction 的部分简译:
模空间的存在性长期以来都作为代数几何的研究热点. 我们对是否存在一类能够"参数化"几何对象的空间感兴趣, 更进一步的, 如果这类空间存在, 它是否能够作为scheme? 它是否proper? coherent sheaf over 的模空间 蕴含了许多 本身的几何信息. 然而, 并不总是存在. 许多情况下, 我们想要参数化的一族对象过"大", 导致 无法成为scheme, 因此我们希望研究有某些特殊性质的coherent sheaf 构成的模空间. 本文讨论的主要为具有固定的Hilbert polynomial 的一族torsion-free sheaf 形成的模空间. 而想要研究这一类模空间, 首先要解决的问题是 这一族coherent sheaf是否有界, 也就是当模空间存在时, 它是否是finite type over base field的.
Hilbert and Quot Functors
WARNING: 本文可能不适合人类阅读, 因为有着一堆跳步以及个人记号.
这篇文章来自于我对moduli space 的一些初步了解. 主要抄了 Birkar 的 Topics in Algebraic Geometry 以及Harvard 的MATH259 的notes.
何谓moduli space? Fine moduli space 即是对moduli functor 的一个representative. 说人话就是对于任意 scheme over base , 我们有 , 这里 是 -points of . 我们同时可以考虑 中的 以及其所对应的 中的元素, 这个 叫做universal family. 取出这个 有什么好处呢? 如果我们考虑 中的另一个元素, 通过一个类似Yoneda lemma 的讨论, 可以证明 是 的一个通过 中的某一个点的pullback, 即这些元素和fibre 能够做出一个对应.
本文中讨论的Hilbert scheme 以及 Quot scheme 就是最为简单的fine moduli space 的例子, 这部分工作被记录与Grothendieck 的FGA. 同样也可以想一想如果把global section functor 作为一个moduli functor, 那么它是否存在fine moduli space 呢? 如果存在, 这个space 是什么以及上面的universal family 又是什么呢?
Ans: and .
UC Berkeley MATH256B Spring 2024
以下是我2024年春季于UC Berkeley 上的MATH256B Algebraic Geometry的一些课程资料.
我不确定是否能将课程作业的答案公开, 如果这些文件侵犯了您的利益请联系我进行删除.
2024 Spring 的代数几何由Prof. Paul Vojta 讲授, 参考教材为Hartshorne 的巨著Algebraic Geometry. Prof. Vojta 大概讲授了 II 6 以及III 1-9 节的内容.
图片为Prof. Vojta 的代表作之一, Mordell 猜想的Diophantine Approximation 证明.
1 / 4