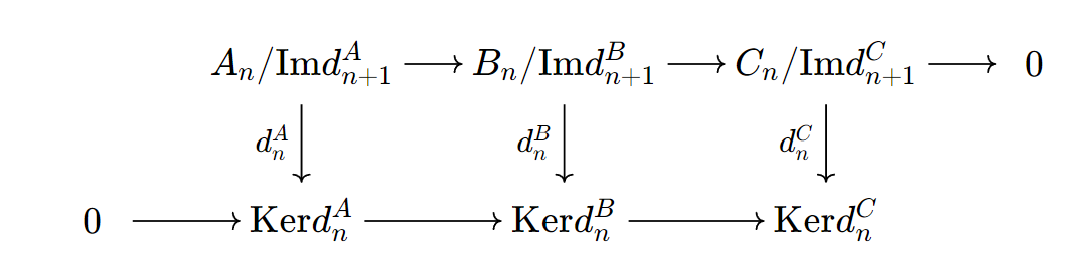Chain Complex

Definition 1. A chain complex $(A,d)$ in an addicitive category $\mathcal{A}$ is a family of objects and morphisms: $$\cdots\xrightarrow{}A_{n+1}\xrightarrow{d_{n+1}}A_{n}\xrightarrow{d_{n}}A_{n-1}\xrightarrow{}\cdots$$ with $d_{i-1}\circ d_{i}=0$ for all $i\in\mathbb{Z}$ .

The family $d$ as well as its components $d_{n}$ is called the
differential of boundary morphism.

Definition 2. A morphism of complexes $f:(A,d^{A})\to (B,d^{B})$ is a family of morphisms: $f_{n}:A_{n}\to B_{n}$ , $n\in \mathbb{Z}$ s.t. the diagram

commutes. To simplify the notation, we always write it as $fd^{A}=d^{B}f$ .

The category of chain complex in $\mathcal{A}$ is denoted $\mathrm{Ch}(\mathcal{A})$ . The full subcategory whose objects are of the form $$\cdots\xrightarrow{}A_{1}\xrightarrow{}A_{0}\xrightarrow{}0\xrightarrow{}\cdots$$ is denoted $\mathrm{Ch}_{\geq 0}(\mathcal{A})$ .

If $\mathcal{A}$ is an addicitive category, it’s easy to verify $\mathrm{Ch}(\mathcal{A})$ is an abelian category.

Proposition 1. For morphism $f:A\to B$ , $f$ is injective(resp. surjective) if and only if $f_{n}:A_{n}\to B_{n}$ is injective(resp. surjective) for all $n$ .

Proof

Proof. Obvious. ◻

Proposition 2. $A\xrightarrow{f}B\xrightarrow{g}C$ is exact if and only if for all $n$ , $A_{n}\xrightarrow{f_{n}}B_{n}\xrightarrow{g_{n}}C_{n}$ are exact.

Proof

Proof. Obvious. ◻

Homology

Definition 3. Let $A$ be a chain complex, the $n$ -th homology group of $A$ is defined to be $H_{n}(A)=\mathrm{Ker}d_{n} /\mathrm{Im}d_{n+1}$ .

From the diagram

we can derive $H(f_{n}):H_{n}(A)\to H_{n}(B)$ by $f_{n}:\mathrm{Ker}d_{n}^{A}\to \mathrm{Ker}d_{n}^{B}$ and $f_{n}:\mathrm{Im}d_{n+1}^{A}\to \mathrm{Im}d_{n+1}^{B}$ and the universal property of quotient. So we see actually $H(-)$ is a functor $H_{n}(-):\mathrm{Ch}(\mathcal{A})\to \mathcal{A}$ .

Often, in particular in applications to topology, elements of chain complex $A_{n}$ are called $n$ -chains; elements of $\mathrm{Ker}d_{n}$ are called $n$ -cycles and $\mathrm{Ker}d_{n}$ is written $Z_n = Z_n(A)$ ; elements of $\mathrm{Im}d_{n+1}$ are called $n$ -boundaries and $\mathrm{Im}d_{n+1}$ is written $B_n = B_n(A)$ . Two $n$ -cycles which determine the same element in $H_n(A)$ are called homologous. The element of $H_n(A)$ determined by the $n$ -cycle $c$ is called the homology class of $c$ , and is denoted by $[c]$ .

Cochain Complex

Definition 4. A chain complex $(A,d)$ in an addicitive category $\mathcal{A}$ is a family of objects and morphisms:

\cdots\xrightarrow{}A^{n-1}\xrightarrow{d_{n-1}}A^{n}\xrightarrow{d^{n}}A^{n+1}\xrightarrow{}\cdots

with $d^{i}\circ d^{i+1}=0$ for all $i\in\mathbb{Z}$ .

The morphisms and cohomology functor is defined similarly.

For a chain complex $A=(A_{n},d_{n}^{A})$ , we can obtain a cochain complex $B=(B^{n},d^{n}_{B})$ by setting $B^{n}=A_{-n}$ and $d^{n}_{B}=d_{-n}^{A}$ .

Long Exact Sequence Theorem

Lemma 1 (Snake lemma). Let $A$ be an abelian category. Let

be a commutative diagram with exact rows.

There exists a unique morphism $\delta:\mathrm{Ker}\gamma\to \mathrm{Coker}\alpha$ s.t. the diagram

commutes, where $\pi'$ , $\pi$ are the canonical projections and $\tau$ , $\tau'$ are the canonical injections.

The induced sequence $$\mathrm{Ker}\alpha\xrightarrow{f’}\mathrm{Ker}\alpha\xrightarrow{f’}\mathrm{Ker}\beta\xrightarrow{g’}\mathrm{Ker}\gamma\xrightarrow{\delta}\mathrm{Coker}\alpha\xrightarrow{k’}\mathrm{Coker}\beta\xrightarrow{l’}\mathrm{Coker}\gamma$$ is exact. If $f$ is injective the so is $f'$ , and if $l$ is surjective then so is $l'$ .

Proof

Proof. See

Stack Project 010H

https://stacks.math.columbia.edu/tag/010H

. ◻

Theorem 1 (Long exact seq.). Given a short exact seq. of chain complexes $0\xrightarrow{}A\xrightarrow{f}B\xrightarrow{g}C\xrightarrow{}0$ , there are connecting morphisms $\delta_{n}:H_{n}(C)\to H_{n-1}(A)$ s.t. $$\cdots\xrightarrow{} H_{n}(A)\xrightarrow{}H_{n}(B)\xrightarrow{}H_{n}( C)\xrightarrow{\delta_{n}}H_{n-1}(A)\xrightarrow{}H_{n-1}(B)\xrightarrow{}H_{n-1}( C)\xrightarrow{}\cdots$$ is an exact sequence.

Proof

Proof. Consider exact sequence:

0\xrightarrow{}A_{n}\xrightarrow{f_{n}}B_{n}\xrightarrow{g_{n}}C_{n}\xrightarrow{}0

Since $f_{n}$ takes $\mathrm{Im}d_{n+1}^{A}$ to $\mathrm{Im}d_{n+1}^{B}$ , $g_{n}$ takes $\mathrm{Im}d_{n+1}^{B}$ to $\mathrm{Im}d_{n+1}^{ C}$ , we have the sequence $$A_{n} /\mathrm{Im}d_{n+1}^{A}\xrightarrow{\bar{f_{n}}} B_{n} /\mathrm{Im}d_{n+1}^{B}\xrightarrow{\bar{g_{n}}}C_{n} /\mathrm{Im}d_{n+1}^{ C}$$ exact. Since $g_{n}$ surjective, $\bar{g_{n}}$ is also surjective. We have the exact sequence $$A_{n} /\mathrm{Im}d_{n+1}^{A}\xrightarrow{\bar{f_{n}}} B_{n} /\mathrm{Im}d_{n+1}^{B}\xrightarrow{\bar{g_{n}}}C_{n} /\mathrm{Im}d_{n+1}^{ C}\xrightarrow{}0$$
Similarly,

0\xrightarrow{}\mathrm{Ker}d_{n}^{A}\xrightarrow{}\mathrm{Ker}d_{n}^{B}\xrightarrow{}\mathrm{Ker}d_{n}^{C}

is an exact sequence.

Since $d_{n}\circ d_{n+1}=0$ , we have $d_{n+1}^{A}$ restrict to $A_{n} /\mathrm{Im}d_{n+1}^{A}$ to $\mathrm{Ker}d_{n}^{A}$ , we get the commutative diagram:

$\mathrm{Ker}(d_{n}^{A}:A_{n} /\mathrm{Im}d_{n+1}^{A}\to \mathrm{Ker}d_{n}^{A})=H_{n}(A)$ and $\mathrm{Coker}(d_{n}^{A}:A_{n} /\mathrm{Im}d_{n+1}^{A}\to \mathrm{Ker}d_{n}^{A})=H_{n-1}(A)$ , by snake lemma, it induces $$\cdots\xrightarrow{} H_{n}(A)\xrightarrow{}H_{n}(B)\xrightarrow{}H_{n}( C)\xrightarrow{\delta_{n}}H_{n-1}(A)\xrightarrow{}H_{n-1}(B)\xrightarrow{}H_{n-1}( C)\xrightarrow{}\cdots$$ ◻

Similarly result for cochain.

For any $[c]\in H_{n}(C)$ , $\exists b\in B_{n}$ s.t. $g_{n}(b)=c$ . Then $g_{n-1}(d_{n}^{B}(b))=d_{n}^{C}(g_{n}(b))$ . $\exists a\in A_{n-1}$ with $f_{n-1}(a)=d_{n}^{B}(b)$ . The map $\delta$ takes $[c]$ to $[a]$ .