Derived Functors

Left Derived Functor

Definition 1. For an object $A$ in abelian category $\mathcal{A}$ and its projective resolution $P$ , let $T:\mathrm{Ch}(\mathcal{A})\to \mathrm{Ch}(\mathcal{A})$ be an addictive functor. We define the left derived functor of $T$ , $L_{n}T(A)=H_{n}(TP)$

$$TP: \quad \cdots \to TP_{n}\to TP_{n-1}\to\cdots\to TP_{0}\to 0$$

From the Revolution we know for $\bar{f}:A\to B$ , the morphism $\bar{f}$ induces $f:P\to Q$ , where $P$ , $Q$ are projective resolution of $A$ , $B$ respectively. So when applying $H(-)$ , the left derived functor is indeed a functor.

Now we verify $L_{n}T(A)$ is well-defined, i.e. for $P, Q$ two projective resolution of $A$ , there’s an isomorphism $L_{n}^{P}T(A)\cong L_{n}^{Q}T(A)$ .

Since the two projective resolutions are of the same homotopy type, i.e. $\exists f:P\to Q$ and $g:Q\to P$ with $fg\simeq id_{Q}$ , $gf\simeq id_{P}$ . Then $Tf$ , $Tg$ gives homotopy equivalence between $TP$ and $TQ$ since $T$ is addictive. Since homotopic morphisms will give the same homology morphisms, we have $H_{n}(TP)\cong H_{n}(TQ)$ , i.e. $L_{n}^{P}T(A)\cong L_{n}^{Q}T(A)$ .

Definition 2. An covariant functor $F$ is left eact if for every exact sequence $0\to A_{1}\to A_{2}\to A_{3}$ , the sequence $0\to FA_{1}\to FA_{2}\to FA_{3}$ is exact.

Definition 3. An covariant functor $F$ is right eact if for every exact sequence $A_{1}\to A_{2}\to A_{3}\to 0$ , the sequence $FA_{1}\to FA_{2}\to FA_{3}\to 0$ is exact.

Definition 4. An covariant functor $F$ is eact if it is left and right exact.

Theorem 1. Let $T:\mathrm{Ch}(\mathcal{A})\to \mathrm{Ch}(\mathcal{A})$ be a right exact functor, then $L_{0}T$ and $T$ are naturally isomorphic.

Proof

Proof. For a projective resolution $P$ of $A$ , applying $T$ to $P$ , we have $TP_{1}\to TP_{0}\to TA\to 0$ exact. So $H_{0}(TP)\cong TA$ . The naturality is obvious. ◻

Proposition 1. The functor $L_{n}T:\mathcal{A}\to\mathcal{A}$ is an addictive functor.

Proof

Proof. Omitted. ◻

Theorem 2. Let $0\to K_{q}\xrightarrow{f} P_{q-1}\to \cdots\to P_{0}\to A\to 0$ be an exact sequence with $P_{q-1},\dots, P_{0}$ projective. If $T$ is right exact, then the sequence

$$0\to L_{q}TA\to TK_{q}\xrightarrow{Tf}TP_{q-1}$$

is exact.

Proof

Proof. Consider $\cdots\to P_{q+1}\to P_{q}\to K_{q}\to 0$ a projective resolution of $K_{q}$ . Then we get an projective resolution of $A$ by

\cdots\to P_{q+1}\to P_{q}\to P_{q-1}\to \cdots\to P_{0}\to A\to 0

Since $T$ is right exact, we consider the diagram

By snake lemma, we get an exact sequence

TP_{q+1}\xrightarrow{Td_{q+1}}\mathrm{Ker}Td_{q}\to \mathrm{Ker}Tf\xrightarrow{\delta}0

By exactness, $\mathrm{Ker}Tf\cong \mathrm{Ker}Td_{q} /\mathrm{Im}Td_{q+1}=H_{q}(TP)$ . ◻

Using duality, we have a similar theorem:

Theorem 3. Let $P_{q}\xrightarrow{d_{q}}P_{q-1}\to \cdots\to P_{0}\to A\to 0$ be an exact sequence, where $P_{q-1}, \dots, P_{0}$ are projective. If $T$ is left exact, then the sequence

$$T(P_{q})\to T(\mathrm{Im}d_{q})\to L_{q-1}T(A)\to 0$$

is exact.

Right Derived Functor

Definition 5. For an object $A$ in abelian category $\mathcal{A}$ and its injective resolution $I$ , let $T:\mathrm{Coch}(\mathcal{A})\to \mathrm{Coch}(\mathcal{A})$ be an addictive functor. We define the right derived functor of $T$ , $R^{n}T(A)=H^{n}(TI)$

$$TI: \quad 0\to TI_{0}\to\cdots\to TI_{q}\to TI_{q+1}\to \cdots$$

Similarly, we can prove $R^{n}T$ is a well-defined functor.

Theorem 4. If $T$ is left exact, then $R^{0}T$ is naturally isomorphic to $T$ .

Proof

Proof. Omitted. ◻

If we choose $T$ to be a controvariant functor, we use the projective resolution $P$ of $A$ to make $TP$ a cochain. Then we will have similar proposition as left derived functor.

Derived Long Exact Sequence

From the long exact sequence theorem, we can derive the following theorems.

Lemma 1 (Horseshoe). For exact sequence $0\to A'\xrightarrow{f}A\xrightarrow{g}A''\to 0$ and projective resolution $P'$ , $P''$ of $A'$ and $A''$ respectively. There exists projective resolution $P$ of $A$ s.t. the following diagram commutes and rows exact.

Proof

Proof. Let $P=P'\oplus P''$ , we have $P$ also a projective and acyclic chain complex. Then $0\to P'\to P\to P''\to 0$ is an exact sequence.

We use induction to build $P\to A\to 0$ .

First for $n=0$ :

By projectivity, we can find $h_{0}:P''_{0}\to A$ with $gh_{0}=d_{0}$ . Since $P_{0}$ is a direct sum and

P'_{0}\xrightarrow{fd_{0}}A\xleftarrow{h_{0}}P''_{0}

we have a unique morphism $d_{0}:P_{0}\to A$ . Using the snake lemma we can conclude $P_{0}\to A\to 0$ exact.

Suppose for $n\geq 1$ , the induction step is exactly the same as $n=0$ . ◻

Now we give the long exact sequence theorem of left derived functor.

Theorem 5. Let $T:\mathrm{Ch}(\mathcal{A})\to \mathrm{Ch}(\mathcal{A})$ be a covariant addictive functor. $0\to A' \to A\to A''\to 0$ is a short exact sequence. Then there are $\omega_{n}:L_{n}TA''\to L_{n-1}TA'$ s.t. the following sequence exact

\cdots\to L_{n}TA'\to L_{n}TA\to L_{n}TA''\to L_{n-1}TA'\to \cdots\to L_{0}TA''\to 0

Proof

Proof. Applying lemma above to we get a commtative dagram with exact rows:

Since $P=P'\oplus P''$ , $T$ is addictive, we have $0\to TP'\to TP\to TP''\to 0$ exact. Using long exact sequence theorem we have the long exact sequence

\cdots\to L_{n}TA'\to L_{n}TA\to L_{n}TA''\to L_{n-1}TA'\to \cdots\to L_{0}TA''\to 0

◻

Let $\theta:T\to T'$ be a natural transformation, we can define morphism $\theta_{P}:TP\to T'P$ . Then $\theta_{P}$ induces a natural transformation $\theta_{A}^{n}:L_{n}TA\to L_{n}T'A$ .

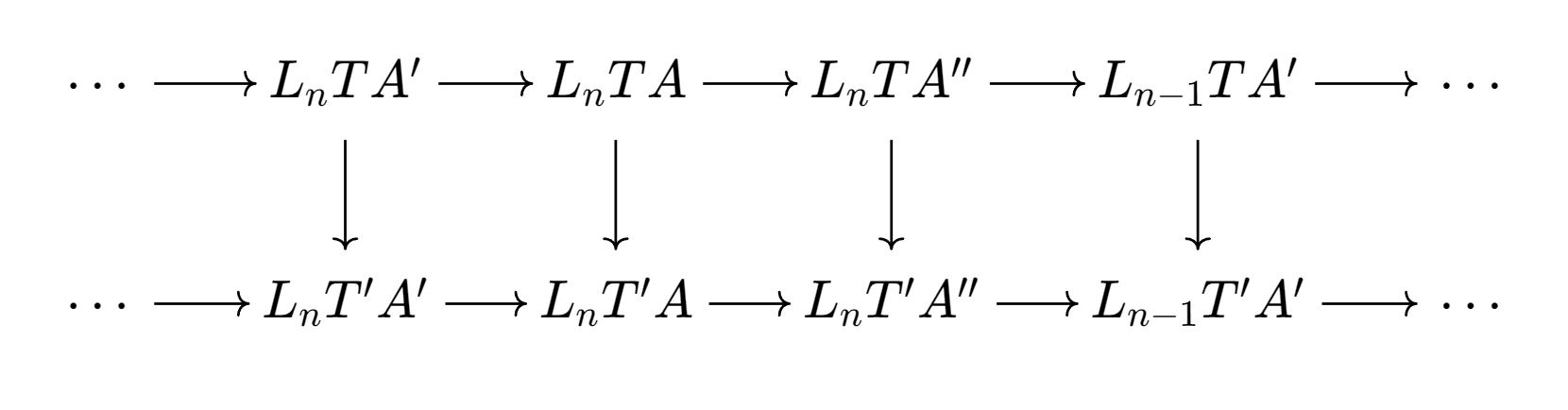
Theorem 6. Let $\theta:T\to T'$ be a natural transformation. The diagram is commtative with exact rows

Then the following diagram commutes with exact rows:

1.

2.

Proof

Proof. Omitted. Using generalized snake lemma. ◻

Definition 6. We say a sequence of functor $0\to T'\to T\to T''\to 0$ exact on projectives if for every projective objects $P$ , the sequence $0\to T'P\to TP\to T''P\to 0$ is exact.

Theorem 7. Let the sequence $0\to T'\to T\to T''\to 0$ be exact on projectives. Then for every object $A$ , there are morphisms $\omega_{n}:L_{n}T''A\to L_{n}T'A$ s.t. there’s long exact sequence

\cdots\to L_{n}T'A\to L_{n}TA\to L_{n}T''A\to L_{n-1}T'A\to \cdots\to L_{0}T''A\to 0

Proof

Proof. Omitted. ◻

Theorem 8. Let $f:A\to A'$ be a morphism and

be a commtative diagram with exact rows on projectives. Then the following diagrams commtutes with exact rows:

1.

2.

Proof

Proof. Omitted. Using generalized snake lemma. ◻