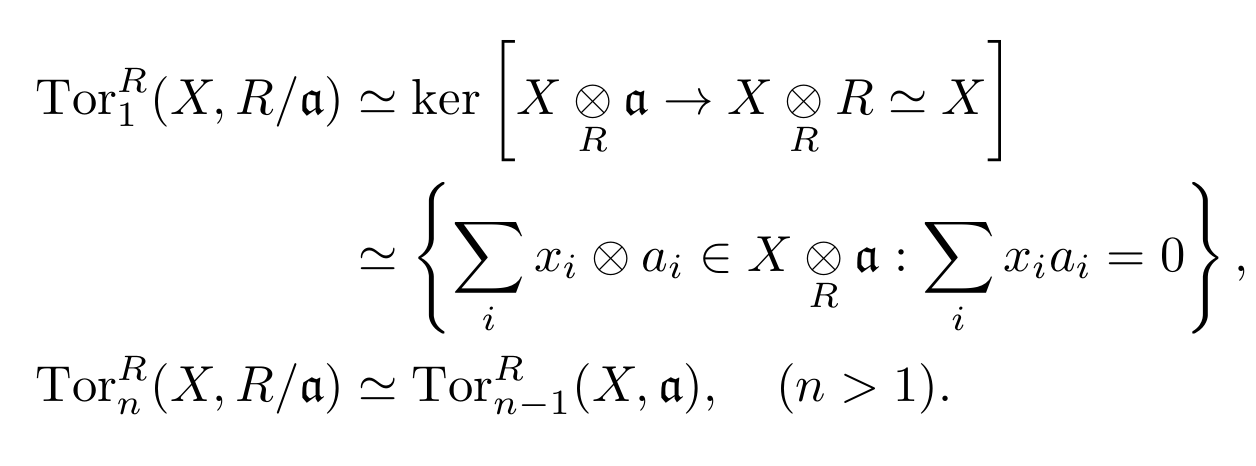这一节Ext函子和Tor函子, 大部分内容是上一章的直接推论, 唯一一个不平凡的定理择时对双函子Hom导出会得到相同的结果. 本节后半部分是关于这俩导出函子的计算的, 这俩函子的计算十分富有技巧性, 全写上来会很长. 最后部分的表格参考了Xiong Rui的小册子.
We consider category with enough projectives, e.g. Mod.
Functor Ext
Definition 1. The extension functor ExtAn(−,B) is given by right derived functor of HomA(−,B), the controvariant functor. I.e. ExtAn(−,B)=RnHomA(−,B).
Since Hom(−,B) is a left exact functor, ExtA0(A,B)≅Hom(A,B), by theorem in Derived Functors.
Proposition 1. If P is projective, I is injective, then ExtAn(P,B)=ExtAn(A,I)=0.
Proof
Proof. For projective resolution O→P, we have
ExtAn(P,B)=Hn(Hom(O,B))=0
For ExtAn(A,I), we check that Hom(−,I) is an exact functor. Only need to show for exact sequence 0→A→B→C→0, Hom(B,I)→Hom(A,I)→0 exact. This is directly from the injectivity. So Hom(−,A) is exact, and RnHom(−,I)=0 for all n≥1. ◻
Proposition 2. For any exact sequence 0→B′→B→B′′→0 and object A, we have the long exact sequence
⋯→ExtAn(A,B′)→ExtAn(A,B)→ExtAn(A,B′′)→ExtAn+1(A,B′)→⋯
Proof
Proof. Immediate corollary from Derived Functors ◻
Functor Extˉ
Definition 2. The extension functor ExtˉAn(A,−) is given by the right derived functor of HomA(A,−), the covariant functor, i.e. ExtˉAn(A,−)=RnHomA(A,−).
Hom(A,−) is a left exact functor so ExtˉA0(A,B)=Hom(A,B).
Theorem 1. The bifunctor ExtAn(−,−) and ExtˉAn(−,−) are naturally equivalent.
Proof
Proof. We use induction to show ExtAn(−,−)≅ExtˉAn(−,−).
For n=1, take an injective presentation 0→B→I→S→0 of B and a projective resolution P of A. Since Pn are all projective, we have
0→Hom(P,B)→Hom(P,I)→Hom(P,S)→0
exact. Applying the right derived functor, we get
Hom(A,I)→Hom(A,S)→ExtA1(A,B)→0=ExtA1(A,I)
exact. Derive the exact sequence 0→B→I→S→0, we also have the exact sequence
Hom(A,I)→Hom(A,S)→ExtA1(A,B)→0=ExtˉA1(A,I)
From the above two exact sequence, ExtA1(A,B)≅ExtˉA1(A,B).
For n≥2, just replace these two exact sequence by
ExtˉAn−1(A,I)→ExtˉAn−1(A,S)→ExtˉAn(A,B)→ExtˉAn(A,I)
and
ExtAn−1(A,I)→ExtAn−1(A,S)→ExtAn(A,B)→ExtAn(A,I)
◻
For exact sequence 0→Rn−1→Pn−1→⋯→P0→A→0, where Pn−1,…,P0 are all projective, then
ExtAn(A,B)=Coker(Hom(Pn−1,B)→Hom(Rn−1,B))
For exact sequence 0→B→I0→⋯→In−1→Sn−1→0, where I0,…,In−1 are all injective, then
ExtAn(A,B)=Coker(Hom(A,In−1)→Hom(A,Sn−1))
These are the corollary of theorem in Derived Functors
Functor Tor
Definition 3. The torsion functor TornA(A,−) is given by the left derived functor of the covariant functor A⊗A−, i.e. TornA(A,−)=Ln(A⊗A−).
Since A⊗− is a right exact functor, we have Tor0A(A,B)=A⊗B.
Similarly, we can define TorˉnA(−,B)=Ln(−⊗B), here −⊗B is a covariant functor.
Theorem 2. The bifunctor TornA(−,−) and TorˉnA(−,−) are naturally equivalent.
Proof
Proof. Similar to the proof of Ext and Extˉ above. Note that every projective module is flat. ◻
Similary to functor Ext, we have following conclusions. For the exact sequence 0→Rn−1→Pn−1→⋯→P0→A→0, where Pn−1,…,P0 are all projective, then
TornA(A,B)=Ker(Rn−1⊗B→Pn−1⊗B)
For the exact sequence 0→Rn−1→Pn−1→⋯→P0→B→0, where Pn−1,…,P0 are all projective, then
TornA(A,B)=Ker(A⊗Rn−1→A⊗Pn−1)
Proposition 3. If A is flat, then for any object P, TornA(A,B)=0. Similar for flat B.
Proof
Proof. For projective resolution P→B→0, A⊗P→A⊗B→0 is also exact. Thus TornA(A,B)=0. ◻
Theorem 3. If object A has flat resolution F→A→0,
$$F\quad \cdots\to F_{2}\to F_{1}\to F_{0}$$
then TornA(A,B)=Hn(F⊗B)
Proof
Proof. We omit this proof and just use it. ◻
Computation fo Ext and Tor
Theorem 4.
-
Hom(⊕iAi,∏jBj)=∏i,jHom(Ai,Bj).
-
ExtAn(⊕iAi,∏jBj)=∏i,jExtAn(Ai,Bj).
-
(⊕iAi)⊗(⊕jBj)=⊕i,j(Ai⊗Bj).
-
TornA(⊕iAi,⊕jBj)=⊕i,jTornA(Ai,Bj).
Proof
Now we focus on Z-Mod, Zn-Mod, Q-Mod and Q/Z-Mod.
For Hom, we have
| Hom(↓,→) |
Zm |
Z |
Q |
Q/Z |
| Zn |
Z(m,n) |
0 |
0 |
Zn |
| Z |
Zm |
Z |
Q |
Q/Z |
| Q |
0 |
0 |
Q |
? |
| Q/Z |
0 |
0 |
0 |
? |
For Ext, we have
| Ext(↓,→) |
Zm |
Z |
Q |
Q/Z |
| Zn |
Z(m,n) |
Zn |
0 |
0 |
| Z |
0 |
0 |
0 |
0 |
| Q |
? |
? |
0 |
0 |
| Q/Z |
? |
? |
0 |
0 |
For ⊗, we have
| ↓⊗Z→ |
Zm |
Z |
Q |
Q/Z |
| Zn |
Z(m,n) |
Zn |
0 |
0 |
| Z |
Zm |
Z |
Q |
Q/Z |
| Q |
0 |
Q |
Q |
0 |
| Q/Z |
0 |
Q/Z |
0 |
0 |
For Tor, we have
| Tor(↓,→) |
Zm |
Z |
Q |
Q/Z |
| Zn |
Z(m,n) |
0 |
0 |
Zn |
| Z |
0 |
0 |
0 |
0 |
| Q |
0 |
0 |
0 |
0 |
| Q/Z |
Zm |
0 |
0 |
Q/Z |
And for those arbitrary abelian group, just apply the structure theorem of finite generated abelian group.