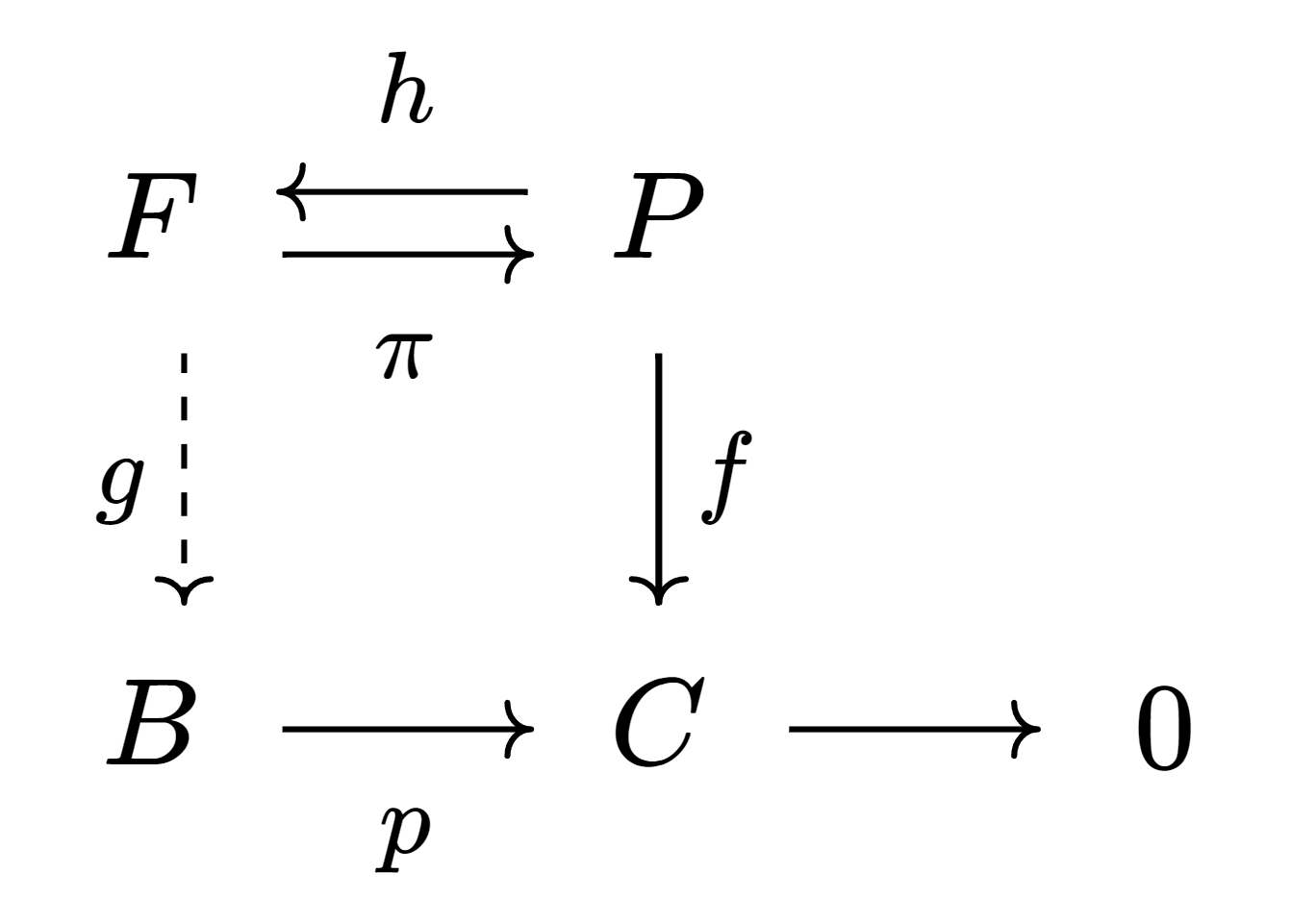Presentation 定理二号, Krull PIT 是维数理论中十分重要的一个定理. 用它可以刻画出Noetherian scheme 上的tangent space 的维数大于等于局部维数的性质, 从而定义那些nonsingular 的点. Hartshorne 第一章就有这个定理, 关于tangent space的讨论则被藏在了习题5.10 里面. 值得注意的是Hartshorne 定理1.8A是一个非常不平凡的结果, 这个定理对于finitely generated $k$ algebra成立, 然而对于一般的catenary ring, 即任何prime ideal chain 长度相等的ring 却不一定成立, 也挺有意思的.

Matsumura 抄书系列. Chevalley 定理是这学期课程里面的某一个presentation内容. 对于一般的情况下, 一个morphism 不一定把一个algebraic set 映射到algebraic set, 但是一个finite type morphism 却能保持constructible sets. 在affine space上的结论就是这个定理的直接推论, 证明起来更简单一些.

局部化和取商是交换代数里面最常用的技巧. 取商能够给出包含理想的理想, 而局部化则能给出素理想内部的理想. 可以通过saturation 来一般地刻画$S^{-1}R$ 中的理想. 而对于module 而言, $S^{-1}(-)$ 这一个函子的正合性十分重要, 这给出了很多局部化module 的商的结果. 同样的, 也可以通过saturation 来刻画$S^{-1}M$ 的子模. 局部环在几何上是在一点处的连续函数germ 空间, 这为我们研究局部环提供了理由.

啥都能水系列

茴字的四种写法之Nakayama lemma. 大定理的最后几个部分和一般的Nakayama lemma (finite 版本)差的有点远了, 但是还是抄上来了.

啥都能水系列

Absolutely flatness 是使得任意module flat 的环, 并没有找到很多的absolutely flat 环, 常见的例子还是有field 和Boolean ring. Absolutely flatness 最大的特征是对任意极大理想局部化后是一个field. 同时absolutely flatness 和Zariski topology 的分离性有很强的关系.

Faithfully flat module 简单理解就是将tensor 前的序列的正合性等价于tensor 后序列的正合性. 比较好的判别法有: tensor非零module 后依旧非零. 在代数几何里面faithfully flatness 可以用来构造平坦下降~~(虽然我不会)~~

Flat module 的第一部分内容, 主要是一部分的判别法. Flatness的性质确实十分多, 并且也没有injective 和projective 那么直观. Atiyah 中还有一个很重要的结果是colimit 会保持exact sequence, 并且colimit 可以和Tor进行交换. 这只是flatness 很小的一部分东西.

Injective 是projective 的对偶, 但是在问题的处理上却复杂得多. 核心原因是我们在处理projective module 时是去寻找一个打到它的满射, 而injective module 则是需要寻找一个从它出发的单射. Zorn引理在这里具有很强的效果. Baer 判别法也是一个很有效的工具.

一些很简单的projective module的内容, 比较有意思的是最后一个定理. 这个这个定理给出了local ring上的finite generated projective module一定是free的. 这是Kaplanski定理的一个特殊情况, 在这里的证明使用了Nakayama引理数维数.

(头图快不够了, 估计以后要用美少女来代替了 (ㄒoㄒ)/)