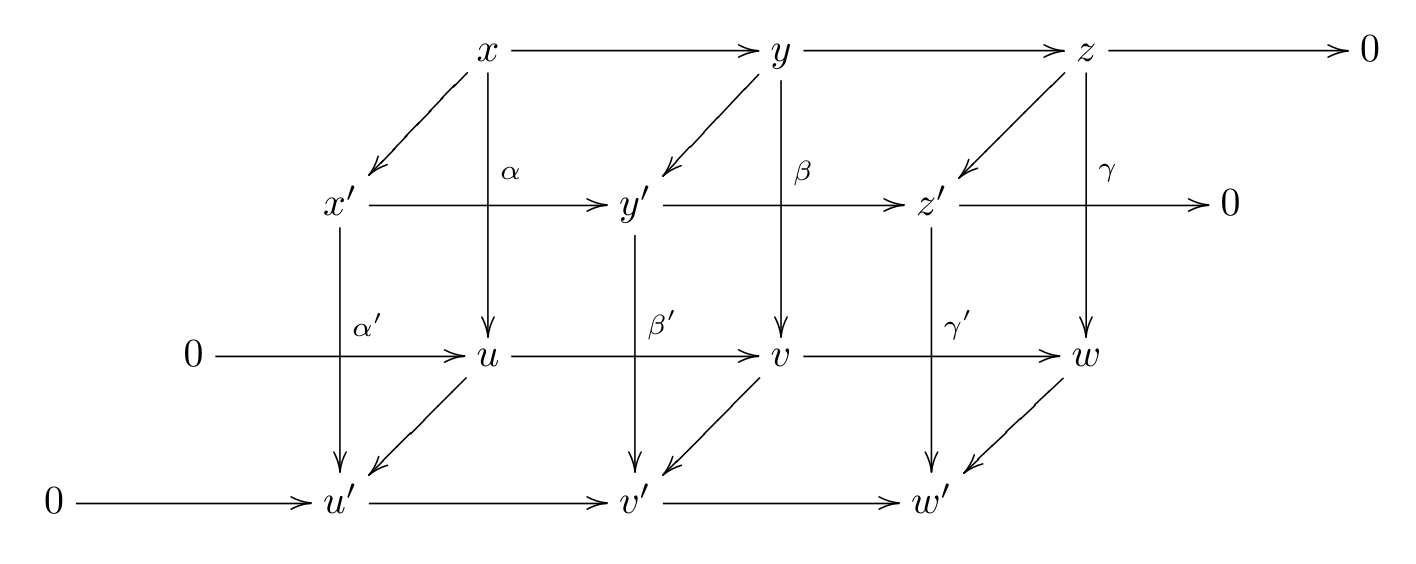
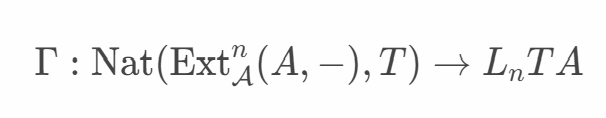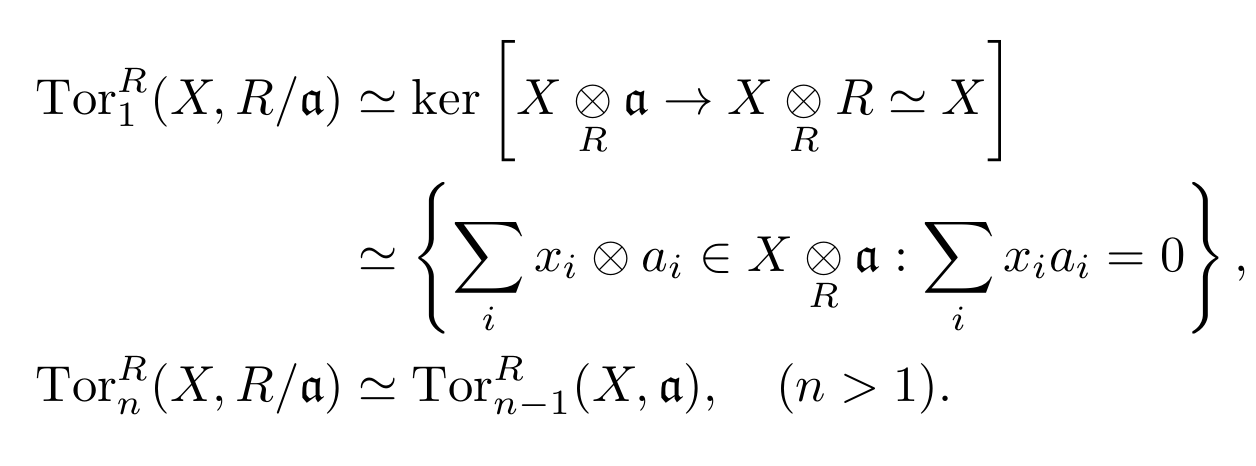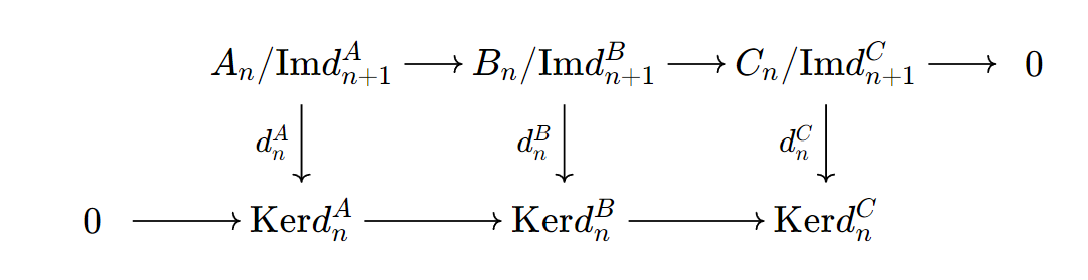这次是kunneth formula, 以及kunneth formula的直接推论, 同调万有系数定理和上同调万有系数定理. 没有学过代数拓扑所以基本上是从直观角度理解这个几个定理: 上同调万有系数定理应用比较直观, 直接给出了homology和cohomology之间的计算以及转换关系. 同调万有系数定理我觉得是在说这样一件事: 在改变定义同调时使用的系数环的情况下同调会发生什么样的变化. 这几个定理的证明说简单也简单, 也就是导出长正合列之后计算的事, 但是说复杂也很复杂, 这几个kernel都不是人算的. 这应该是一辈子只需要证明一次的定理, 使用比证明更加重要. P.S. kunneth formula 的证明可能有一点bug.(;′⌒`)
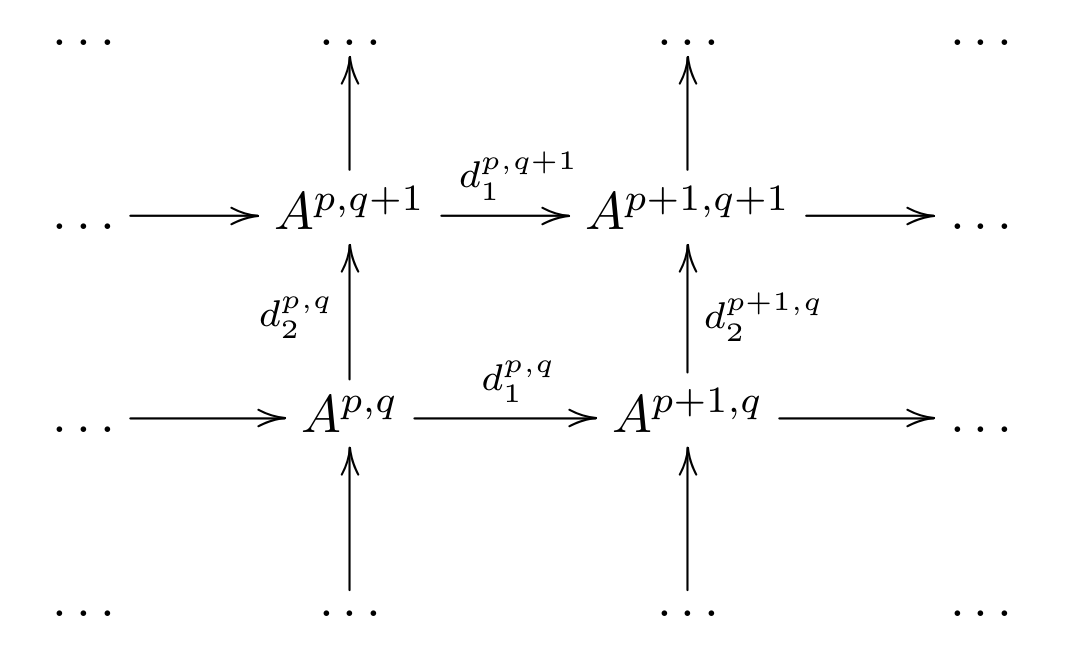
Double Complex
这部分是double complex的一些内容, 内容比较少, 主要就是为了给后面的kunneth formula有个基本的定义啥的, 不考虑Tot函子的整体性质整块内容也没啥需要证明的, 摸了.👻 Stack Project 里面有很全的内容.
Homological Yoneda Lemma
Yoneda lemma的同调代数版本. 这是个很神奇的事情, 可以通过natural transformation 和Ext函子来计算一些函子的左导出函子. 整体的证明参考了论文The Yoneda isomorphism commutes with homology
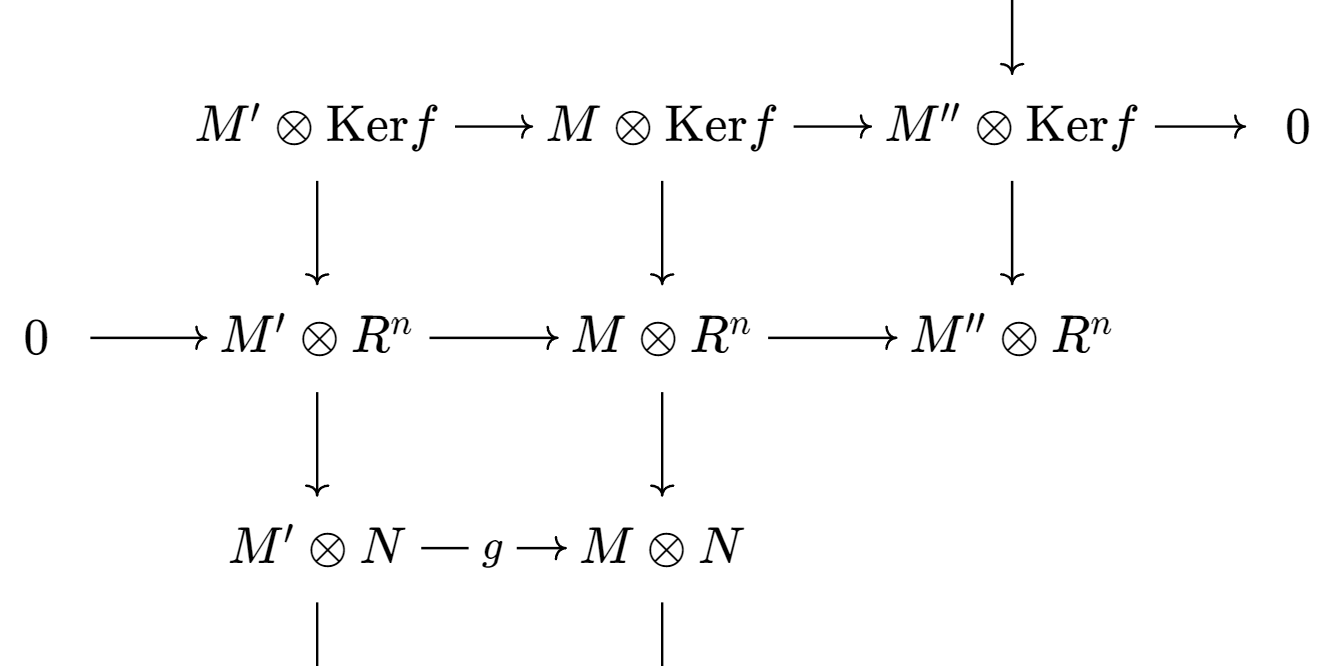
Ext functor and Tor functor
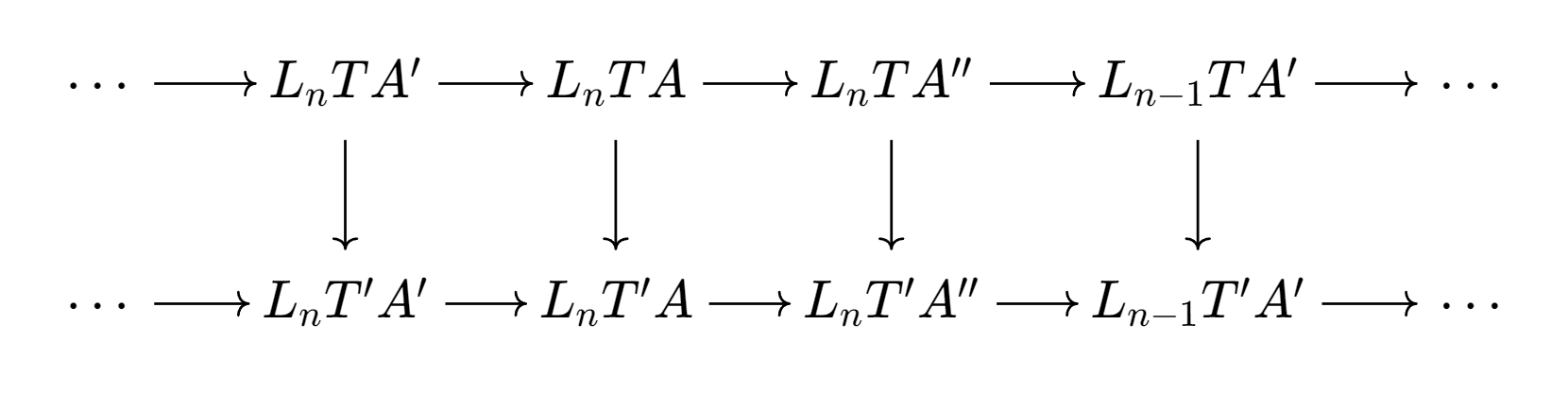
这一节Ext函子和Tor函子, 大部分内容是上一章的直接推论, 唯一一个不平凡的定理择时对双函子Hom导出会得到相同的结果. 本节后半部分是关于这俩导出函子的计算的, 这俩函子的计算十分富有技巧性, 全写上来会很长. 最后部分的表格参考了Xiong Rui的小册子.
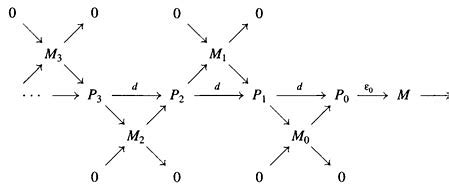
Resolution
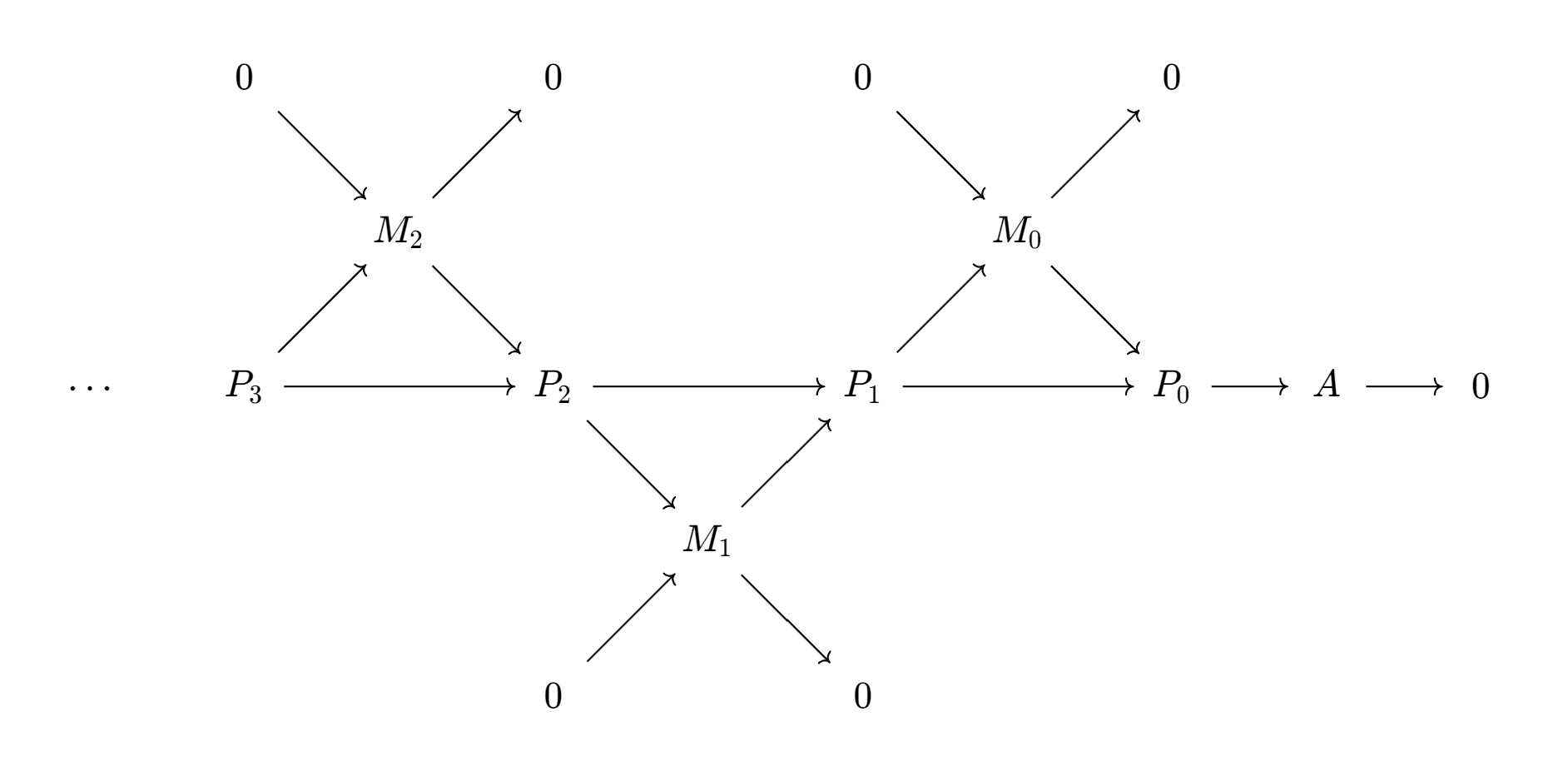
Resolution, 构造projective, injective, free和flat解消能够用来计算一系列导出函子. Resolution也是定义导出函子的前置. 这一节主要考虑projective resolution.
Homotopy
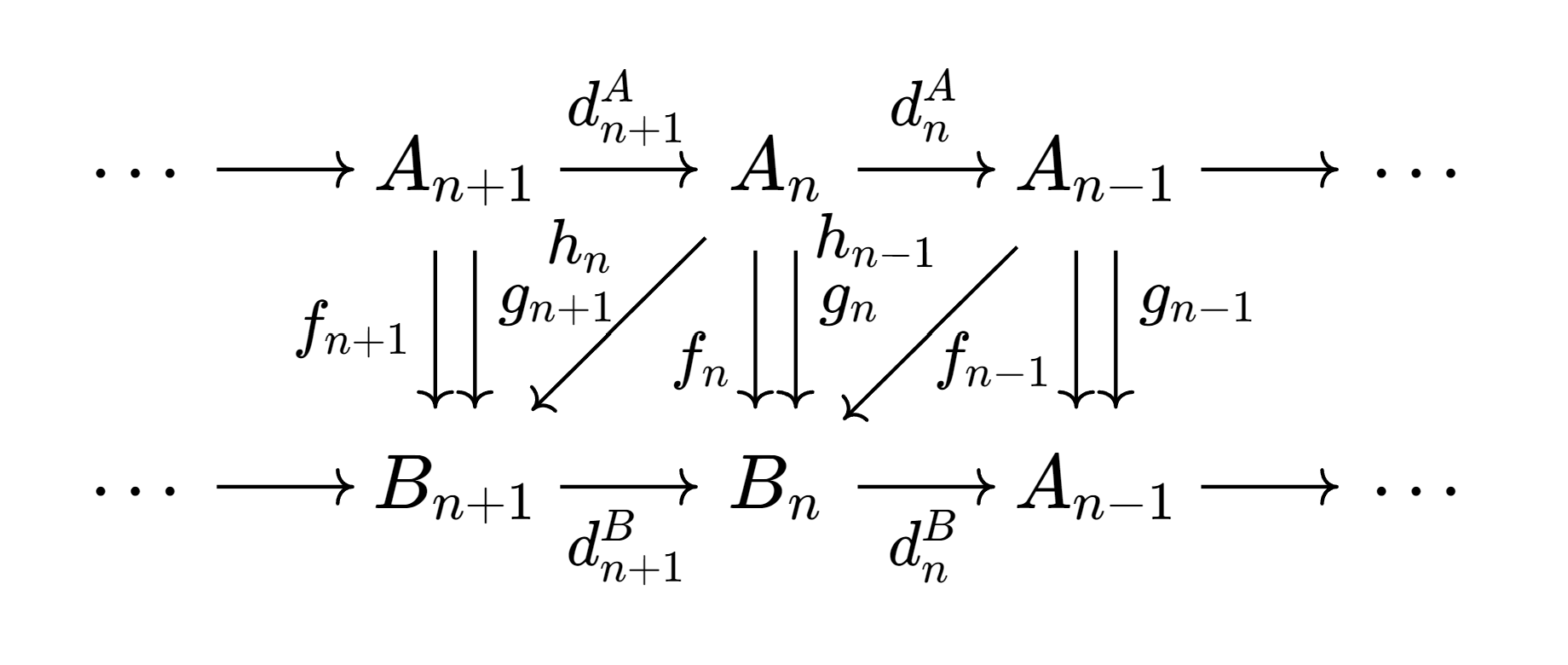
Homological algebra初步, 对一些homotopy性质的讨论. Homology函子将homotopic的morphism映射到相同的morphism, 这是以后讨论homotopy需要用到的最根本的性质之一.
以及这个homotopy定义实在是抽象.
An example of direct sum but not split exact sequence
一个含有direct sum的short exact sequence但不是split short exact sequence的例子.