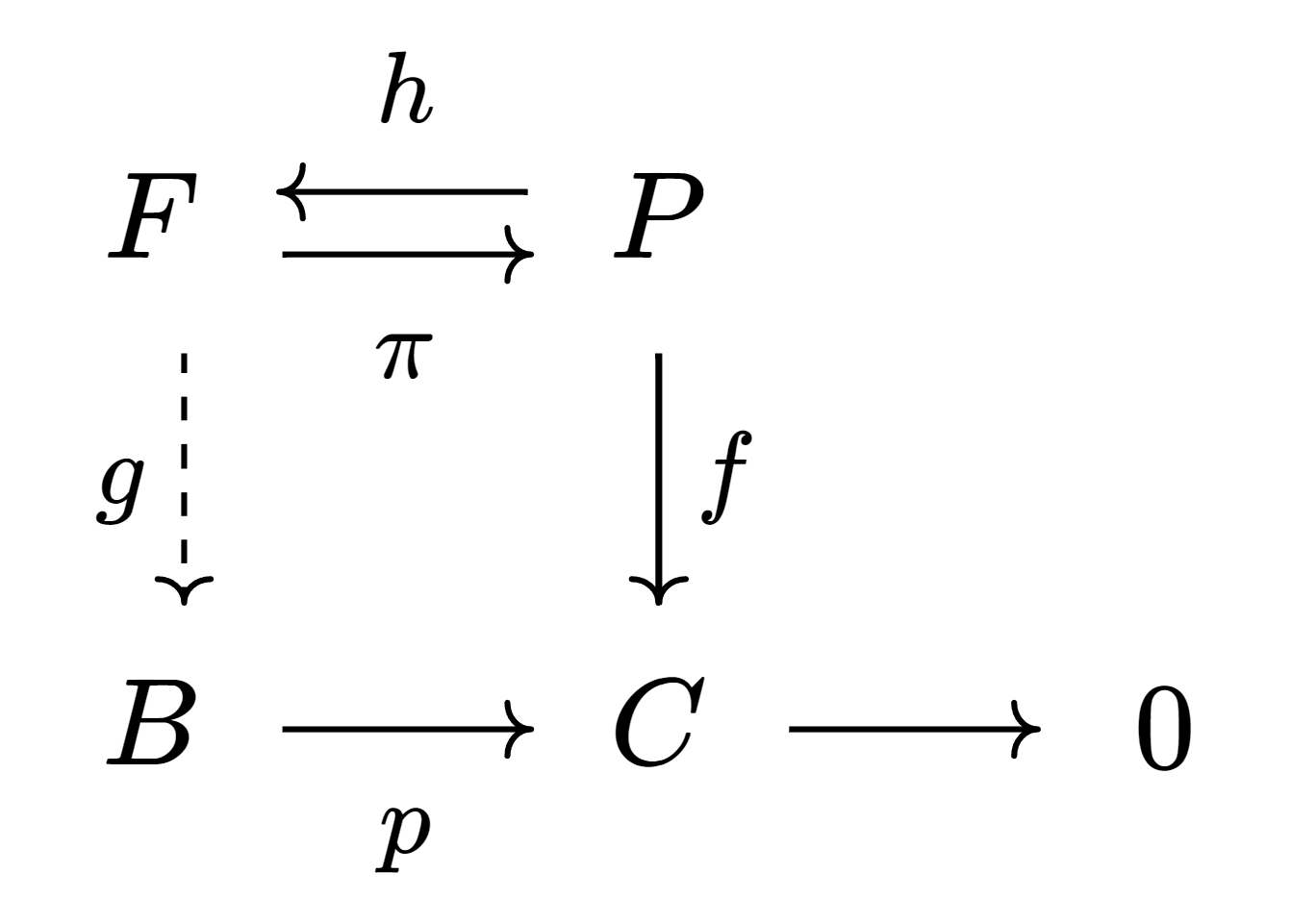Flat module 的第一部分内容, 主要是一部分的判别法. Flatness的性质确实十分多, 并且也没有injective 和projective 那么直观. Atiyah 中还有一个很重要的结果是colimit 会保持exact sequence, 并且colimit 可以和Tor进行交换. 这只是flatness 很小的一部分东西.
Injective Module
Injective 是projective 的对偶, 但是在问题的处理上却复杂得多. 核心原因是我们在处理projective module 时是去寻找一个打到它的满射, 而injective module 则是需要寻找一个从它出发的单射. Zorn引理在这里具有很强的效果. Baer 判别法也是一个很有效的工具.
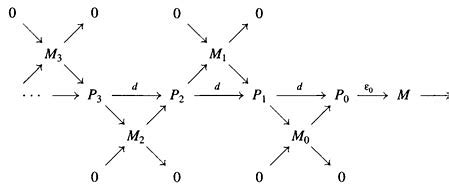
Projective Module
一些很简单的projective module的内容, 比较有意思的是最后一个定理. 这个这个定理给出了local ring上的finite generated projective module一定是free的. 这是Kaplanski定理的一个特殊情况, 在这里的证明使用了Nakayama引理数维数.
(头图快不够了, 估计以后要用美少女来代替了 (ㄒoㄒ)/)
An example of direct sum but not split exact sequence
一个含有direct sum的short exact sequence但不是split short exact sequence的例子.